Introduction
Environmental exposures often show a time-lagged association with outcomes [1–3]. Distributed lag models have been used to capture such lag patterns by incorporating time-lagged values of exposures, with the corresponding of the lag structure approximated by polynomials or splines [1, 4]. These models require the correct input of cut-off time, or pre-specified window (hereafter termed lag length), after which the association diminishes to a constant level, typically zero [5, 6]. However, lag length is often unknown [5–7]. To fit distributed lag models without specifying lag length, we revisit transfer functions (TFs), a method to specify time-lagged associations commonly used in econometrics and introduced to epidemiology in 1991 [8–10]. We provide a case study to capture the time-lagged association between weekly purchasing outcome of sugar-sweetened drinkable yogurt and weekly-varying display promotion of these beverages, which is an obesogenic food environmental exposure in supermarkets.
Methods
TFs capture a time-lagged exposure-outcome association using a structural variable, denoted Et, which summarizes the current association (at time t) and cumulative association (up to time t) between the outcome variable Yt and time-lagged exposure variable Xt−1 + Xt−2 + Xt−3+... [8, 11] (Supplementary Appendix S1). We illustrate a simple form of TF to capture a commonly observed shape of lag pattern, a monotonically decreasing association of outcome and lagged exposure, often called the Koyck decay [12]. Using the decay coefficient of lagged association λ up to lag h, the decreasing associations are represented as which recursively reduces to
The coefficient β captures the immediate association at time t, and the value of decay coefficient λ closer to 1 implies a more persistent association over time (i.e., slower decay), while a value closer to zero indicates a shorter lag [12, 13]. Constraining λ to be 0 < λ < 1 ensures the association monotonically decaying towards zero when the value of β is positive (Supplementary Figure S1A), and previous studies also imposed the decay towards zero [14, 15]. The variable Et is added to a time-series regression for the outcome Yt to estimate β and λ as Yt = Et + Ztγ + εt, where Zt represents a set of covariates and intercept with coefficients γ, and εt represents the error term [10, 13].
A visual interpretation of a lagged association combining these coefficients is provided by an impulse response function (IRF), representing the change of the outcome Yt+0 + Yt+1 + Yt+2 + … + Yt+h to an impulse (one-unit increase of x at time t only), while holding other variables constant [16]. The IRF of the Koyck decay is β + βλ1 + βλ2 + … + βλh, visualized in Figure 1.
FIGURE 1
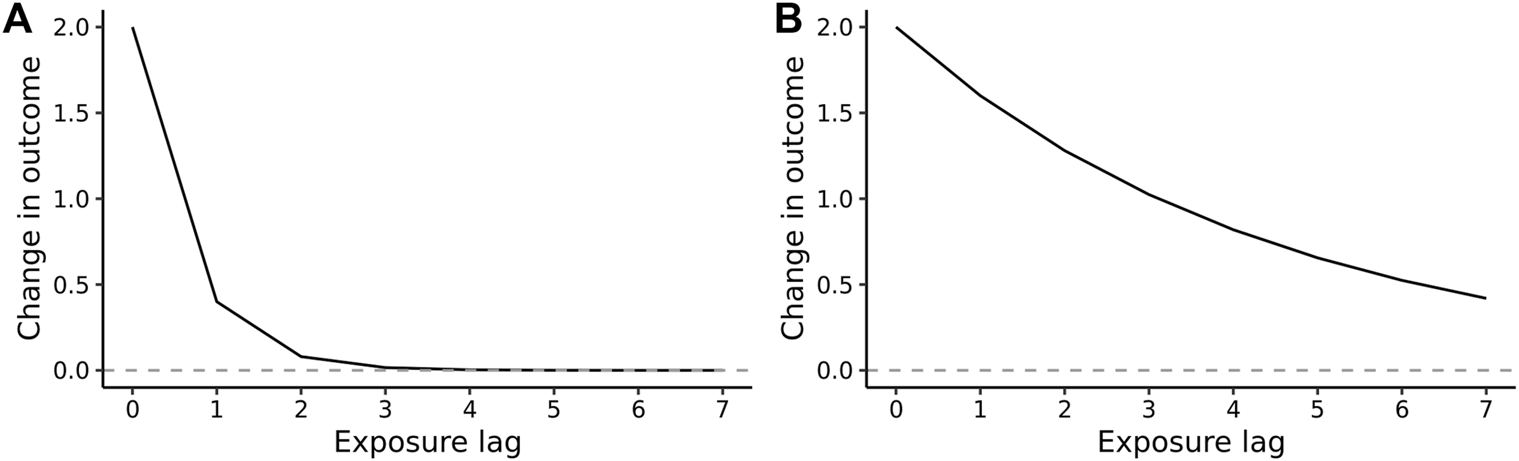
Hypothetical impulse response function of the Koyck lag transfer function, with the rate and extent of decay being controlled by the value of the lag parameter λ: (A) a weak decay returning to the baseline with a short lag (λ = 0.2): (B) a more persistent lag, i.e., slower decay (λ = 0.8). The value of the immediate effect, β, at the time of exposure (x = 0) is 2.0 in both plots (Hypothetical function, 2022).
The general specification of the TF capturing various shapes of lag structure iswhere the Koyck decay is captured by p = 0, q = 1 in Eq. 1 above. More complex shapes are specified by higher values of p and q (Figure 2; Supplementary Appendix S2), allowing generalization to classical lag models, such as the Almon polynomial [10, 17].
FIGURE 2
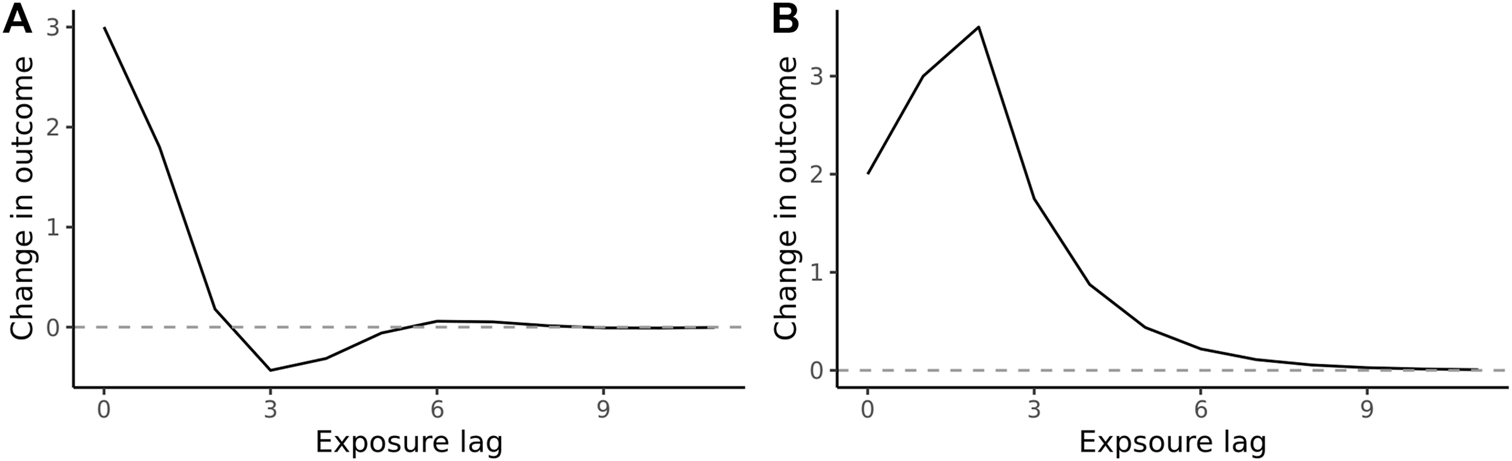
Hypothetical impulse response function of (A) short-term negative association (a “dip” below zero) following the decay of positive association and (B) delayed peak of positive association (Hypothetical function, 2022).
Unlike commonly used distributed lag models, TF models obviates pre-specification of a lag length h, but require prior biological and epidemiological knowledge to help select plausible shapes of the lag (values of p and q). Deciding among candidate shapes is facilitated by model selection using fit metrics such as an information criterion [11].
Case Study
The exposure is the weekly within-store display promotion of sugar-sweetened food items that potentially exhibits time-lagged association with the number of these items sold (outcome). Display promotion is the temporary placement of items in prominent locations to increase sales of (typically) ultra-processed food [18]. Our food of interest is sugar sweetened (not plain) drinkable yogurt, a hidden and important source of dietary sugar among children [19, 20]. A time series of weekly proportion of display-promoted sugar-sweetened drinkable yogurt items (continuous exposure) and weekly sum of the sales quantity of these items (continuous outcome) are recorded from a large supermarket in Montreal, Canada over T = 311 weeks (6 years). Supplementary Appendix S3 and Supplementary Figures S2, S3 elaborate the definition of the exposure and outcome.
The time-series regression used in this study is a dynamic linear model [21, 22]. We added the structural variable, Et, covariates, a seasonal term, and an intercept. We selected the Koyck lag TF (p = 0, q = 1) for Et, since the promotion exposure is likely to have a monotonically decaying association with purchasing [6]. The model was fit under the Bayesian framework as described in Supplementary Appendix S4.
The estimated immediate effect of the TF β was 0.68 (95% Posterior Credible Interval [CI]: 0.39–0.96), implying two-fold increase in sales at week t, if all yogurt items were display- promoted in the same week. The point estimate of the decay coefficient λ was moderately strong: 0.47 (95% CI 0.20–0.72), as shown by the distinct lag in the estimated IRF (Figure 3). Residual diagnostics indicate the absence of temporally autocorrelated residuals (Supplementary Figure S4).
FIGURE 3
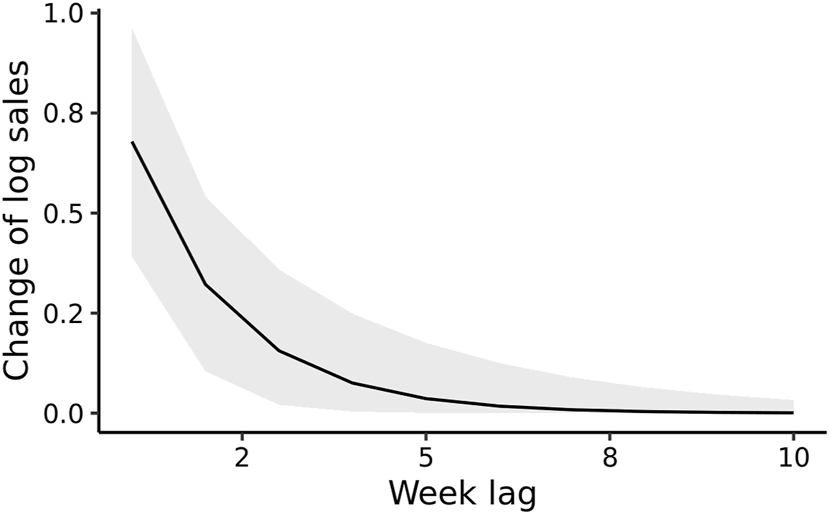
The estimated impulse response function of display promotion on the (natural log) sales of sugar-sweetened drinkable yogurt, based on the lag parameters β and λ learned from the time-series of sales data from a single store (Montreal, Canada, 2008–2013). The grey band indicates pointwise 95% posterior credible interval. The immediate association is displayed at lag 0 and is 0.68 (95% Posterior Credible Interval: 0.39–0.96), indicating that the immediate impact of display promotion is a doubling of sales, since exp(0.68) = 1.97.
Discussion
Time-lagged exposure-outcome associations are of critical interest in time-series analysis. We described TF modeling to estimate lagged associations when lag length is unknown a priori. Previous applications of TFs include environmental time-series analysis to capture decaying associations between arbovirus incidence and temperature [23] and interrupted time-series analysis to capture the persistent effect of interventions [11, 24]. TF modeling requires pre-specification of the shape of a lag structure from investigators’ prior knowledge followed by their selection based on model fit. When such knowledge is lacking, existing distributed lag models such as those using splines allow data-driven estimation of the shape of lag. They require the specification of lag length by model selection applied to plausible lag lengths [25], by setting a long enough length to cover the unobserved true lag window with a potential sacrifice of precision [4], or alternatively estimating the lag length from data [26, 27]. Limitations of TFs include challenges in selecting the most appropriate shape of lag, when competing shapes show similar model fit. Finally, a comprehensive evaluation of TFs to capture lagged associations from simulated environmental health data is warranted, including their capacities to capture non-linear exposure-outcome associations by making β time-varying (dynamic) or imposing non-linear structure to Et [17, 28].
Statements
Ethics statement
The studies involving human participants were reviewed and approved by the McGill University, Faculty of Medicine, Institutional Review Board. Written informed consent from the participants’ legal guardian/next of kin was not required to participate in this study in accordance with the institutional requirements.
Author contributions
The study was conceived and designed by HM and was reviewed and approved by the other authors. Authors AMS and EEMM provided inputs on the statistical analysis and interpretation of the results. Author DLB provided the data and computational resources. Data analysis and drafting of manuscript was led by HM. All authors reviewed, provided critical comments to the manuscript, and approved the final version of the manuscript for submission.
Funding
This study was funded by an Institut de valorisation des données (IVADO) post-doctoral fellowship.
Acknowledgments
The study has been disseminated as a preprint at MedRxiv [29].
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Supplementary material
The Supplementary Material for this article can be found online at: https://www.ssph-journal.org/articles/10.3389/ijph.2022.1604841/full#supplementary-material
References
1.
Bhaskaran K Gasparrini A Hajat S Smeeth L Armstrong B . Time Series Regression Studies in Environmental Epidemiology. Int J Epidemiol (2013) 42(4):1187–95. 10.1093/ije/dyt092
2.
Schwartz J . The Distributed Lag between Air Pollution and Daily Deaths. Epidemiology (2000) 11(3):320–6. 10.1097/00001648-200005000-00016
3.
Gasparrini A Armstrong B Kenward MG . Distributed Lag Non-linear Models. Statist Med (2010) 29(21):2224–34. 10.1002/sim.3940
4.
Gasparrini A . Modelling Lagged Associations in Environmental Time Series Data. Epidemiology (2016) 27(6):835–42. 10.1097/ede.0000000000000533
5.
Wang P Zhang X Hashizume M Goggins WB Luo C . A Systematic Review on Lagged Associations in Climate-Health Studies. Int J Epidemiol (2021) 50(4):1199–212. 10.1093/ije/dyaa286
6.
Hanssens DM, Parsons LJ, Schultz RL , editors. Design of Dynamic Response Models. Market Response Models [Internet]. Boston, MA: Springer US (2001). p. 139–82. 10.1007/0-306-47594-4_4
7.
Guo Y Gasparrini A Armstrong BG Tawatsupa B Tobias A Lavigne E et al Heat Wave and Mortality: a Multicountry, Multicommunity Study. Environ Health Perspect (2017) 125(8):087006. 10.1289/ehp1026
8.
Helfenstein U . The Use of Transfer Function Models, Intervention Analysis and Related Time Series Methods in Epidemiology. Int J Epidemiol (1991) 20(3):808–15. 10.1093/ije/20.3.808
9.
Box GEP Jenkins GM Reinsel GC Ljung GM . Chapter 11: Transfer Function Models. In: Time Series Analysis: Forecasting and Control. 5th ed.Hoboken, New Jersey: Wiley (2015).
10.
Ravines RR Schmidt AM Migon HS . Revisiting Distributed Lag Models through a Bayesian Perspective. Appl Stoch Models Bus Ind (2006) 22(2):193–210. 10.1002/asmb.628
11.
Schaffer AL Dobbins TA Pearson SA . Interrupted Time Series Analysis Using Autoregressive Integrated Moving Average (ARIMA) Models: a Guide for Evaluating Large- Scale Health Interventions. MC Med Res Methodol (2021) 21(1):58. 10.1186/s12874-021-01235-8
12.
Koyck LM . Distributed Lags and Investment Analysis. In: Advanced Macroeconomics. 4th ed.Amsterdam: North-Holland Publishing (1954).
13.
West M Harrison J . Regression, Transfer Function and Noise Models. In: West,MHarrisonJ, editors. Bayesian Forecasting and Dynamic Models. New York, NY: Springer (1997). p. 273–318.
14.
Peng RD Dominici F Welty LJ . A Bayesian Hierarchical Distributed Lag Model for Estimating the Time Course of Risk of Hospitalization Associated with Particulate Matter Air Pollution. J R Stat Soc Ser C (Applied Statistics) (2009) 58(1):3–24. 10.1111/j.1467-9876.2008.00640.x
15.
Welty LJ Peng RD Zeger SL Dominici F . Bayesian Distributed Lag Models: Estimating Effects of Particulate Matter Air Pollution on Daily Mortality. Biometrics (2009) 65(1):282–91. 10.1111/j.1541-0420.2007.01039.x
16.
Hamilton JD . Chapter 11. Vector Autoregressions. In: Time Series Analysis. Princeton University Press (1994). p. 291–349.
17.
Alves MB Gamerman D Ferreira MA . Transfer Functions in Dynamic Generalized Linear Models. Stat Model (2010) 10(1):03–40. 10.1177/1471082x0801000102
18.
Hecht AA Perez CL Polascek M Thorndike AN Franckle RL Moran AJ . Influence of Food and Beverage Companies on Retailer Marketing Strategies and Consumer Behavior. Int J Environ Res (2020) 17(20):7381. 10.3390/ijerph17207381
19.
Moore JB Horti A Fielding BA . Evaluation of the Nutrient Content of Yogurts: a Comprehensive Survey of Yogurt Products in the Major UK Supermarkets. BMJ Open (2018) 8:e021387. 10.1136/bmjopen-2017-021387
20.
Langlois K Garriguet D Gonzalez A Sinclair S Colapinto CK . Change in Total Sugars Consumption Among Canadian Children and Adults. Health Rep (2019) 30(1):10–9.
21.
West M Harrison J . Bayesian Forecasting and Dynamic Models. 2nd ed. New York: Springer (1997).
22.
Petris G Petrone S Campagnoli P . Dynamic Linear Models with R. New York: Springer-Verlag (2009).
23.
Freitas LP Schmidt AM Cossich W Cruz OG Carvalho MS . Spatio-temporal Modelling of the First Chikungunya Epidemic in an Intra-urban Setting: The Role of Socioeconomic Status, Environment and Temperature. Plos Negl Trop Dis (2021) 15(6):e0009537. 10.1371/journal.pntd.0009537
24.
Zhou X Crippa A Danielsson AK Galanti MR Orsini N . Effect of Tobacco Control Policies on the Swedish Smoking Quitline Using Intervention Time-Series Analysis. BMJ Open (2019) 9(12):e033650. 10.1136/bmjopen-2019-033650
25.
Armstrong B . Models for the Relationship between Ambient Temperature and Daily Mortality. Epidemiology (2006) 17(6):624–31. 10.1097/01.ede.0000239732.50999.8f
26.
Heaton MJ Peng RD . Flexible Distributed Lag Models Using Random Functions with Application to Estimating Mortality Displacement from Heat-Related Deaths. J Agric Biol Environ Stat (2012) 17(3):313–31. 10.1007/s13253-012-0097-7
27.
Heaton MJ Peng RD . Extending Distributed Lag Models to Higher Degrees. Biostatistics (2014) 15(2):398–412. 10.1093/biostatistics/kxt031
28.
Ravines RR Schmidt AM Migon HS Rennó CD . A Joint Model for Rainfall–Runoff: The Case of Rio Grande Basin. J Hydrol (2008) 353(1):189–200. 10.1016/j.jhydrol.2008.02.008
29.
Mamiya H Schmidt AM Moodie EEM Buckeridge DL . Transfer Functions: Learning About a Lagged Exposure-Outcome Association in Time-Series Data. medRxiv[Preprint] (2021). Available from: https://www.medrxiv.org/content/10.1101/2021.09.30.21264361v1.
Summary
Keywords
time-series analysis, lagged association, environmental exposure, transfer function, food marketing, sugar-sweetened food, dynamic linear model, Bayesian analysis
Citation
Mamiya H, Schmidt AM, Moodie EEM and Buckeridge DL (2022) Revisiting Transfer Functions: Learning About a Lagged Exposure-Outcome Association in Time-Series Data. Int J Public Health 67:1604841. doi: 10.3389/ijph.2022.1604841
Received
16 February 2022
Accepted
17 June 2022
Published
11 July 2022
Volume
67 - 2022
Edited by
Ana Maria Vicedo Cabrera, University of Bern, Switzerland
Reviewed by
Antonio Gasparrini, University of London, United Kingdom
Benedict Armstrong, University of London, United Kingdom
Updates
Copyright
© 2022 Mamiya, Schmidt, Moodie and Buckeridge.
This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Hiroshi Mamiya, hiroshi.mamiya@mail.mcgill.ca
Disclaimer
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.