The Philosophy of the P-value
The p-value, a landmark statistical tool dating from the 18th century, remains a widely used measure in inferential statistics, representing the probability of obtaining a result at least as extreme as the observed one, given that the null hypothesis () is true [1–4]. It operates under the assumption that holds but doesn’t directly assess the validity of the null hypothesis or the likelihood that the observed results occurred by chance [5]. One of its major advantages is that its interpretation is intuitive: the smaller the p-value, the less likely it is that the observed results are compatible with the null hypothesis [6].
However, the p-value has significant limitations. For instance, p-value is sensitive to the sample size. By increasing the sample size, the power of the test increases. Therefore, in very large samples, even minor and clinically irrelevant effects can yield statistically significant p-values, while important effects might go undetected in smaller samples [1].
Alternatively, for a wide range of statistical tests, lowering the significance threshold reduces the chance of false positives, but would also require an increase in sample sizes to maintain the same power [7].
Moreover, relying on a fixed threshold to determine significance can lead to binary interpretations of results (significant vs. not significant) that fail to capture the continuum of statistical evidence. This challenge led researchers to integrate the analyses with additional metrics, such as confidence intervals, that provide a range of values derived from the sample data within which the population value is likely to fall [8–11].
Lastly, the p-value itself provides no information regarding the evidence in favor of an alternative hypothesis. While a small p-value, according to confidence intervals, may suggest that the data do not support , it fails to quantify from a comparative perspective how much more likely the data are under an alternative hypothesis , leaving researchers without a clear measure of relative evidence between the hypotheses [12].
Widespread misusages concerning the p-value encourage statisticians to explore alternative approaches, such as the Bayes Factor [13]. For further insights on the limitations and misconceptions about the p-value, see also [14–17].
Understanding Bayes-Factor
The Bayesian approach to hypothesis testing was developed by Jeffreys in 1935 [18, 19]. The method, now referred to as Bayes Factor (BF), is a Bayesian tool used to compare the evidence in favor of two hypotheses. It compares the likelihood of the data under the null hypothesis to the likelihood under the alternative hypothesis . Therefore, unlike the p-value, the BF directly measures how likely the data are under each hypothesis, providing a quantitative comparison between and [12].
The BF converts prior odds, that represent the ratio of the initial probabilities assigned to the two hypotheses before observing the data, to posterior odds by incorporating the data (). Formally, the BF can be defined as the ratio of the probability of observing the data given and the probability of observing the data given .
Several categorizations were proposed in the form of ratio and compared [12, 18, 20–22]. By considering Formula 1, the BF value can be interpreted as shown in Table 1.
TABLE 1
| BF valuea | Interpretation |
|---|---|
| <0.01 | strong to very strong evidence for H0 |
| 0.01–0.03 | strong evidence for H0 |
| 0.03–0.1 | moderate to strong evidence for H0 |
| 0.1–0.33 | weak to moderate evidence for H0 |
| 0.33–1 | negligible evidence for H0 |
| 1 | no evidence |
| 1–3 | negligible evidence for H1 |
| 3–10 | weak to moderate evidence for H1 |
| 10–30 | moderate to strong evidence for H1 |
| 30–100 | strong evidence for H1 |
| >100 | strong to very strong evidence for H1 |
Guidelines for interpreting the bayes factor (Naples, Italy. 2025).
The researcher should be aware that this scale applies when H1 is in the numerator.
One notable advantage of the BF is its ability to provide a continuous measure of evidence supporting or opposing a hypothesis and its values varies, from strong support for to strong support for [21].
Another benefit is that the BF allows the incorporation of prior information, such as pre-existing knowledge or theoretical assumptions into the analyses, enhancing the robustness of the results.
The data-based BF finds a critical limitation in its sensitivity to the prior choice [21]. Therefore, it is crucial to set priors on a solid pre-existing knowledge or to select them in a conservative way [18]. Alternative methodological approaches to the BF are discussed in [23–26].
Comparing P-Value and Bayes-Factor: A Simulation Study
In literature, many authors focus their research on the comparative study of p-value and BF. Reader can refer to a brief literature review provided in the Supplementary Material [21, 27–35]. Moreover, BF is implemented in various R packages, which offer diverse functionalities for their computation [36–39].
Simulation Design
The simulation proposed in this work was designed to evaluate the behavior of the p-value and the BF in a two-sample t-test comparing the means of two groups. Comprehensive details on how the simulation was conducted are included in the Supplementary Material.
Results
Figure 1 showed the comparative results between p-value and BF in the simulation study. In particular, the medians of p-value and BF simulated distributions were reported. In general, the BF is less sensitive to sample size in the presence of mild effects of 0.1 and 0.2. It can also be observed that the p-value takes an extremely low value in the presence of an effect of 0.5 for a sample size of 150, meanwhile the BF is more cautious since it supports moderate evidence in favor of the alternative hypothesis. Moreover, when the effect size is at 0.5 and is 100, the p-value corroborates the rejection of the null hypothesis, while the evidence for from the BF is barely worth mentioning. However, the p-value is sensitive to sample size only when the null hypothesis is false, while BF seems to be affected by sample size both in the presence and absence of true effects.
FIGURE 1
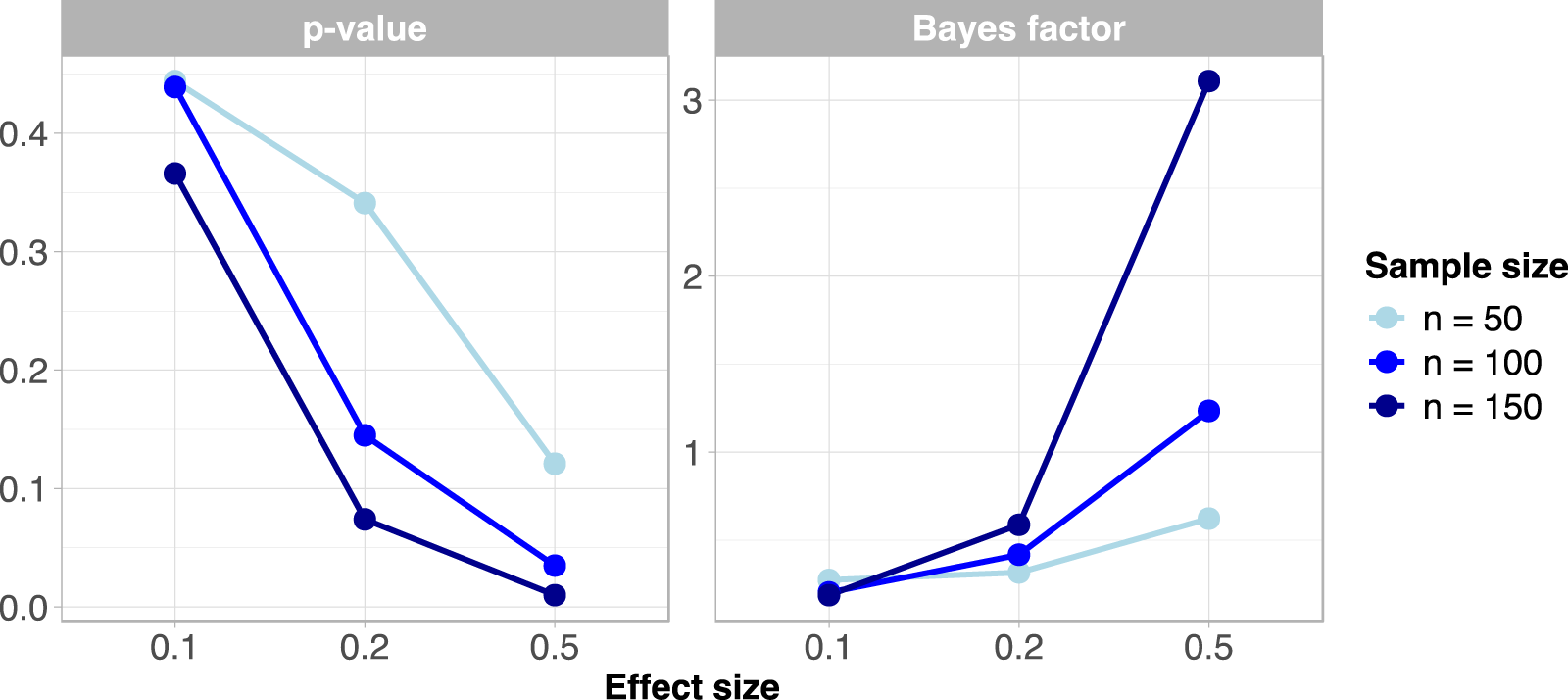
Comparing results between p-value and Bayes factor in the simulation study (Naples, Italy. 2025).
Concluding Remarks
This paper presents a comparison between p-value and BF in hypothesis testing, accompanied by a concise literature review on the subject. Findings from our simulation study align with existing literature, revealing that p-values are more sensitive to variations in sample size and effect size compared to BF. Moreover, BF provide a more nuanced approach to decision-making, offering flexibility beyond the binary accept/reject framework of the null hypothesis. Nevertheless, a controversial aspect is that BF are sensitive to the choice of prior distribution, which can decisively impact the results, especially in more complex settings where researchers must be particularly careful in their implementation.
Statements
Author contributions
Conceptualization, MF, PS, and GN; methodology, MF, PS, and GN; software, MF; validation, MF, PS, GN, SS, and PC; formal and statistical analysis, MF, PS, and GN; writing—original draft preparation, MF, SS, and PC; writing – review and editing, MF, SS, and PC; supervision, SS and PC. All authors contributed to the article and approved the submitted version.
Funding
The author(s) declare that no financial support was received for the research and/or publication of this article.
Conflict of interest
The authors declare that they do not have any conflicts of interest.
Generative AI statement
The authors declare that no Generative AI was used in the creation of this manuscript.
Supplementary material
The Supplementary Material for this article can be found online at: https://www.ssph-journal.org/articles/10.3389/ijph.2025.1608258/full#supplementary-material
References
1.
Chen OY Bodelet JS Saraiva RG Phan H Di J Nagels G et al The Roles, Challenges, and Merits of the P Value. Patterns (2023) 4(12):100878. 10.1016/j.patter.2023.100878
2.
Fisher RA . Statistical Methods and Scientific Inference. 3rd ed. New York: Hafner Press (1973).
3.
Lehmann EL . The Fisher, Neyman–Pearson Theories of Testing Hypotheses: One Theory or Two?J Am Stat Assoc (1993) 88:1242–9. 10.1080/01621459.1993.10476404
4.
Pearson K . On the Criterion that a Given System of Deviations From the Probable in the Case of a Correlated System of Variables Is Such that It Can Be Reasonably Supposed to Have Arisen From Random Sampling. Philos Mag A (1900) 50:157–75.
5.
Goodman SN . Toward Evidence-Based Medical Statistics. 1: The P Value Fallacy. Ann Intern Med (1999) 130(12):995–1004. 10.7326/0003-4819-130-12-199906150-00008
6.
Casella G Berger GL . Statistical Inference. 2nd ed. Pacific Grove: Brooks/Cole (2001).
7.
Benjamin DJ Berger JO Johannesson M Nosek BA Wagenmakers EJ Berk R et al Redefine Statistical Significance. Nat Hum Behav (2018) 2(1):6–10. 10.1038/s41562-017-0189-z
8.
Altman DG . Confidence Intervals in Research Evaluation. Ann Intern Med (1992) 116.
9.
Betensky RA . The P-Value Requires Context, Not a Threshold. The Am Statistician (2019) 73(Suppl. 1):115–7. 10.1080/00031305.2018.1529624
10.
Gardner MJ Altman DG . Confidence Intervals rather Than P Values: Estimation rather Than Hypothesis Testing. BMJ (1986) 292:746–50. 10.1136/bmj.292.6522.746
11.
Greenland S Senn SJ Rothman KJ Carlin JB Poole C Goodman SN et al Statistical Tests, P Values, Confidence Intervals, and Power: A Guide to Misinterpretations. Eur J Epidemiol (2016) 31(4):337–50. 10.1007/s10654-016-0149-3
12.
Goodman SN . Toward Evidence-Based Medical Statistics. 2: The Bayes Factor. Ann Intern Med (1999) 130(12):1005–13. 10.7326/0003-4819-130-12-199906150-00019
13.
Wasserstein RL Lazar NA . The ASA Statement on P-Values: Context, Process, and Purpose. Am Statistician (2016) 70:129–33. 10.1080/00031305.2016.1154108
14.
Amrhein V Greenland S McShane B . Scientists Rise up against Statistical Significance. Nature (2019) 567(7748):305–7. 10.1038/d41586-019-00857-9
15.
Berger JO Sellke T . Testing a Point Null Hypothesis: The Irreconcilability of P Values and Evidence. J Am Stat Assoc (1987) 82(397):112–22. 10.2307/2289131
16.
Browner WS Newman TB . Are All Significant P Values Created Equal? The Analogy between Diagnostic Tests and Clinical Research. Jama (1987) 257(18):2459–63. 10.1001/jama.1987.03390180077027
17.
Goodman S . A Dirty Dozen: Twelve P-Value Misconceptions. Semin Hematol (2008) 45(3):135–40. 10.1053/j.seminhematol.2008.04.003
18.
Kass RE Raftery AE . Bayes Factors. J Am Stat Assoc (1995) 90(430):773–95. 10.2307/2291091
19.
Jeffreys H . Some Tests of Significance, Treated by the Theory of Probability. Math Proc Cambridge Phil|philos Soc (1935) 31(2):203–22. 10.1017/s030500410001330x
20.
Held L Ott M . How the Maximal Evidence of P-Values against Point Null Hypotheses Depends on Sample Size. The Am Statistician (2016) 70(4):335–41. 10.1080/00031305.2016.1209128
21.
Held L Ott M . On P-Values and Bayes Factors. Annu Rev Stat Its Appl (2018) 5(1):393–419. 10.1146/annurev-statistics-031017-100307
22.
Jeffreys H . The Theory of Probability. 3rd ed. Oxford University Press (1961).
23.
Edwards W Lindman H Savage LJ . Bayesian Statistical Inference for Psychological Research. Psychol Rev (1963) 70(3):193–242. 10.1037/h0044139
24.
Hung HJ O'Neill RT Bauer P Köhne K . The Behavior of the P-Value when the Alternative Hypothesis Is True. Biometrics (1997) 53:11–22. 10.2307/2533093
25.
Johnson VE . Bayes Factors Based on Test Statistics. J R Stat Soc Ser B: Stat Methodol (2005) 67(5):689–701. 10.1111/j.1467-9868.2005.00521.x
26.
Johnson VE . Properties of Bayes Factors Based on Test Statistics. Scand J Stat (2008) 35(2):354–68. 10.1111/j.1467-9469.2007.00576.x
27.
Etzioni RD Kadane JB . Bayesian Statistical Methods in Public Health and Medicine. Annu Rev Public Health (1995) 16(1):23–41. 10.1146/annurev.pu.16.050195.000323
28.
Goodman SN . Of P-Values and Bayes: A Modest Proposal. Epidemiology (2001) 12(3):295–7. 10.1097/00001648-200105000-00006
29.
Ioannidis JP . Effect of Formal Statistical Significance on the Credibility of Observational Associations. Am J Epidemiol (2008) 168(4):374–90. 10.1093/aje/kwn156
30.
Wakefield J . Bayes Factors for Genome‐wide Association Studies: Comparison with P‐values. Genet Epidemiol The Official Publ Int Genet Epidemiol Soc (2009) 33(1):79–86. 10.1002/gepi.20359
31.
Pastore M Altoè G . Bayes Factor e P-Value: Così Vicini, Così Lontani. Giornale italiano di psicologia (2013) 40(1):175–94.
32.
Lin R Yin G . Bayes Factor and Posterior Probability: Complementary Statistical Evidence to P-Value. Contemp Clin trials (2015) 44:33–5. 10.1016/j.cct.2015.07.001
33.
Stern HS . A Test by Any Other Name: P Values, Bayes Factors, and Statistical Inference. Multivariate Behav Res (2016) 51(1):23–9. 10.1080/00273171.2015.1099032
34.
Assaf AG Tsionas M . Bayes Factors vs. P-Values. Tourism Management (2018) 67:17–31. 10.1016/j.tourman.2017.11.011
35.
Quatto P Ripamonti E Marasini D . Beyond P<. 05: A Critical Review of New Bayesian Proposals for Assessing the P-Value. J Biopharm Stat (2022) 32(2):308–29. 10.1080/10543406.2021.2009497
36.
Morey RD Rouder JN . Using the BayesFactor Package Version 0.9. 2+ (2015).
37.
Mulder J Gu X Olsson-Collentine A Tomarken A Böing-Messing F Hoijtink H et al BFpack: Flexible Bayes Factor Testing of Scientific Theories in R. arXiv preprint arXiv:1911.07728 (2019). Available online at: https://arxiv.org/pdf/1911.07728. (Accessed 2019).
38.
Linde M van Ravenzwaaij D . Baymedr: An R Package and Web Application for the Calculation of Bayes Factors for Superiority, Equivalence, and Non-inferiority Designs. BMC Med Res Methodol (2023) 23(1):279. 10.1186/s12874-023-02097-y
39.
Tendeiro JN Hoekstra R Wong TK Kiers HA . Introduction to the Bayes Factor: A Shiny/R App. In: Teaching Statistics (2024).
Summary
Keywords
bayes factor, p-value, hypothesis testing, bayesian analysis, bayesian approach
Citation
Fordellone M, Schiattarella P, Nicolao G, Signoriello S and Chiodini P (2025) Decision Rules in Frequentist and Bayesian Hypothesis Testing: P-Value and Bayes Factor. Int. J. Public Health 70:1608258. doi: 10.3389/ijph.2025.1608258
Received
17 December 2024
Accepted
01 May 2025
Published
14 May 2025
Volume
70 - 2025
Edited by
Olaf von dem Knesebeck, University Medical Center Hamburg-Eppendorf, Germany
Reviewed by
Daniel Ludecke, University Medical Center Hamburg-Eppendorf, Germany
Matthias Nübling, FFAW GmbH, Germany
One reviewer who chose to remain anonymous
Updates
Copyright
© 2025 Fordellone, Schiattarella, Nicolao, Signoriello and Chiodini.
This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Mario Fordellone, mario.fordellone@unicampania.it
†These authors have contributed equally to this work and share first authorship
‡These authors share last authorship
Disclaimer
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.